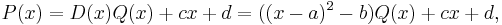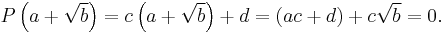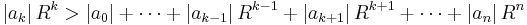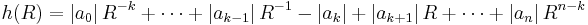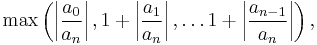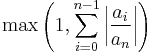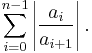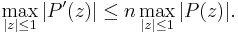Properties of polynomial roots

In mathematics, a polynomial is a function of the form

p(x) = a_0 %2B a_1 x %2B \cdots %2B a_n x^n, \quad x\in \mathbb{C}

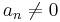where the coefficients a_0, \ldots, a_n are complex numbers and a_n\neq 0. The fundamental theorem of algebra states that polynomial p has n roots. The aim of this page is to list various properties of these roots.

Contents

Continuous dependence of coefficients

The n roots of a polynomial of degree n depend continuously on the coefficients. This means that there are n continuous functions r_1,\ldots, r_n depending on the coefficients that parametrize the roots with correct multiplicity.

This result implies that the eigenvalues of a matrix depend continuously on the matrix. A proof can be found in Tyrtyshnikov(1997).

The problem of approximating the roots given the coefficients is ill-conditioned. See, for example, Wilkinson's polynomial.

Complex conjugate root theorem

Main article: Complex conjugate root theorem

The complex conjugate root theorem states that if the coefficients of a polynomial are real, then the roots appear in pairs of the type a ± ib.

For example, the equation x2 + 1 = 0 has roots ±i.

Radical conjugate roots

It can be proved that if a polynomial P(x) with rational coefficients has a + √b as a root, where a, b are rational and √b is irrational, then a − √b is also a root. First observe that

\left(x - \left [ a %2B \sqrt b \right ] \right) \left(x - \left [ a - \sqrt b \right ] \right) = (x - a)^2 - b.

Denote this quadratic polynomial by D(x). Then, by the division transformation for polynomials,

P(x) = D(x)Q(x) %2B cx %2B d = ((x - a)^2 - b)Q(x) %2B cx %2B d, \,\!

where c, d are rational numbers (by virtue of the fact that the coefficients of P(x) and D(x) are all rational). But a + √b is a root of P(x):

P\left( a %2B \sqrt b \right) = c\left(a %2B \sqrt b \right) %2B d = (ac %2B d) %2B c \sqrt b = 0.

It follows that c, d must be zero, since otherwise the final equality could be arranged to suggest the irrationality of rational values (and vice versa). Hence P(x) = D(x)Q(x), for some quotient polynomial Q(x), and D(x) is a factor of P(x).[1]

Bounds on (complex) polynomial roots

Based on the Rouché theorem

A very general class of bounds on the magnitude of roots is implied by the Rouché theorem. If there is a positive real number R and a coefficient index k such that

|a_k|\,R^k > |a_0|%2B\cdots%2B|a_{k-1}|\,R^{k-1}%2B|a_{k%2B1}|\,R^{k%2B1}%2B\cdots%2B|a_n|\,R^n

then there are exactly k (counted with multiplicity) roots of absolute value less than R. For k=0,n there is always a solution to this inequality, for example

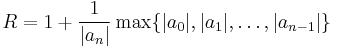R=1%2B\frac1{|a_n|}\max\{|a_0|,|a_1|,\dots, |a_{n-1}|\} or
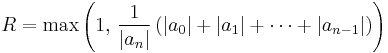
R=\max\left(1,\,\frac1{|a_n|}\left(|a_0|%2B|a_1|%2B\cdots%2B|a_{n-1}|\right)\right)
are upper bounds for the size of all roots,
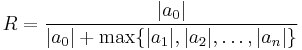R=\frac{|a_0|}{|a_0|%2B\max\{|a_1|,|a_2|,\dots, |a_{n}|\}} or
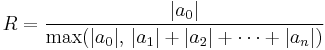
R=\frac{|a_0|}{\max(|a_0|,\,|a_1|%2B|a_2|%2B\cdots%2B|a_{n}|)}

are lower bounds for the size of all of the roots.

h(R)=|a_0|\,R^{-k}%2B\cdots%2B|a_{k-1}|\,R^{-1}-|a_k|%2B|a_{k%2B1}|\,R%2B\cdots%2B|a_n|\,R^{n-k}
is convex on the positive real numbers, thus the minimizing point is easy to determine numerically. If the minimal value is negative, one has found additional information on the location of the roots.

One can increase the separation of the roots and thus the ability to find additional separating circles from the coefficients, by applying the root squaring operation of the Dandelin-Graeffe iteration to the polynomial.

A different approach is by using the Gershgorin circle theorem applied to some companion matrix of the polynomial, as it is used in the Weierstraß–(Durand–Kerner) method. From initial estimates of the roots, that might be quite random, one gets unions of circles that contain the roots of the polynomial.

Other bounds

Useful bounds for the magnitude of all polynomial's roots [2] include the near optimal Fujiwara bound

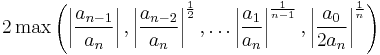2 \max \left( \left|\frac{a_{n-1}}{a_n}\right|,\left|\frac{a_{n-2}}{a_n}\right|^\frac 1 2, \dots \left|\frac{a_1}{a_n}\right|^\frac{1}{n-1}, \left|\frac{a_0}{2a_n}\right|^\frac 1 n\right) (Fujiwara's bound),

which is an improvement (as the geometric mean) of

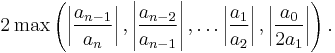2 \max \left( \left|\frac{a_{n-1}}{a_n}\right|,\left|\frac{a_{n-2}}{a_{n-1}}\right|, \dots \left|\frac{a_1}{a_2}\right|, \left|\frac{a_0}{2a_1}\right|\right). (Kojima's bound)

Other bounds are

\max\left(\left|\frac{a_0}{a_n}\right|,1%2B\left|\frac{a_1}{a_n}\right|,\dots 1%2B\left|\frac{a_{n-1}}{a_n}\right|\right),
\max\left(1,\sum_{i=0}^{n-1} \left|\frac{a_i}{a_n}\right|\right)

or

\sum_{i=0}^{n-1} \left|\frac{a_i}{a_{i%2B1}}\right|.

Gauss–Lucas theorem

Main article: Gauss–Lucas theorem

The Gauss–Lucas theorem states that the convex hull of the roots of a polynomial contains the roots of the derivative of the polynomial.

A sometimes useful corollary is that if all roots of a polynomial have positive real part, then so do the roots of all derivatives of the polynomial.

A related result is the Bernstein's inequality. It states that for a polynomial P of degree n with derivative P′ we have

\max_{|z| \leq 1} \big|P'(z)\big| \le n \max_{|z| \leq 1} \big|P(z)\big|.

Polynomials with real roots

If 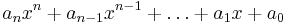a_n x^n%2Ba_{n-1}x^{n-1}%2B\ldots%2Ba_1x%2Ba_0 is a polynomial such that all of its roots are real, then they are located in the interval with endpoints

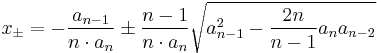x_\pm=-\frac{a_{n-1}}{n\cdot a_n} \pm \frac{n-1}{n\cdot a_n}\sqrt{a^2_{n-1} - \frac{2n}{n-1}a_n a_{n-2}}.

Example: The polynomial 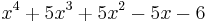x^4%2B5x^3%2B5x^2-5x-6 has four real roots -3, -2, -1 and 1. The formula gives

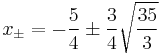x_\pm=-\frac{5}{4} \pm \frac{3}{4}\sqrt{\frac{35}{3}},

its roots are contained in

I = [-3.8117 ; 1.3117].

See also

Notes

  1. ^ S. Sastry (2004). Engineering Mathematics. PHI Learning. pp. 72–73. ISBN 8120325796. 
  2. ^ M. Marden (1966). Geometry of Polynomials. Amer. Math. Soc.. ISBN 0821815032. 

References